Binomial heap / Binomial Tree

https://en.wikipedia.org/wiki/Binomial_heap

Binomial heap - Wikipedia

 

이 글은 위의 위키피디아 글 + 그 외 검색을 통해 얻은 자료들을 요약한 것이다.

 

 

Binomial heap은 binomial tree의 집합으로 이해하면 된다. 그리고 다음과 같은 규칙이 있다.

 

1 ) A binomial tree of orfer 0 is a single node.

2) A binomial tree of order k has a root node whose childeren are roots of binary trees of order k-1,k-2,...,1,0

 

 

 

 

이 규칙이 말로만 보면 잘 이해가 안갈 수도 있는데 이미지로 확인하면 이해가 잘된다.

 

 

 

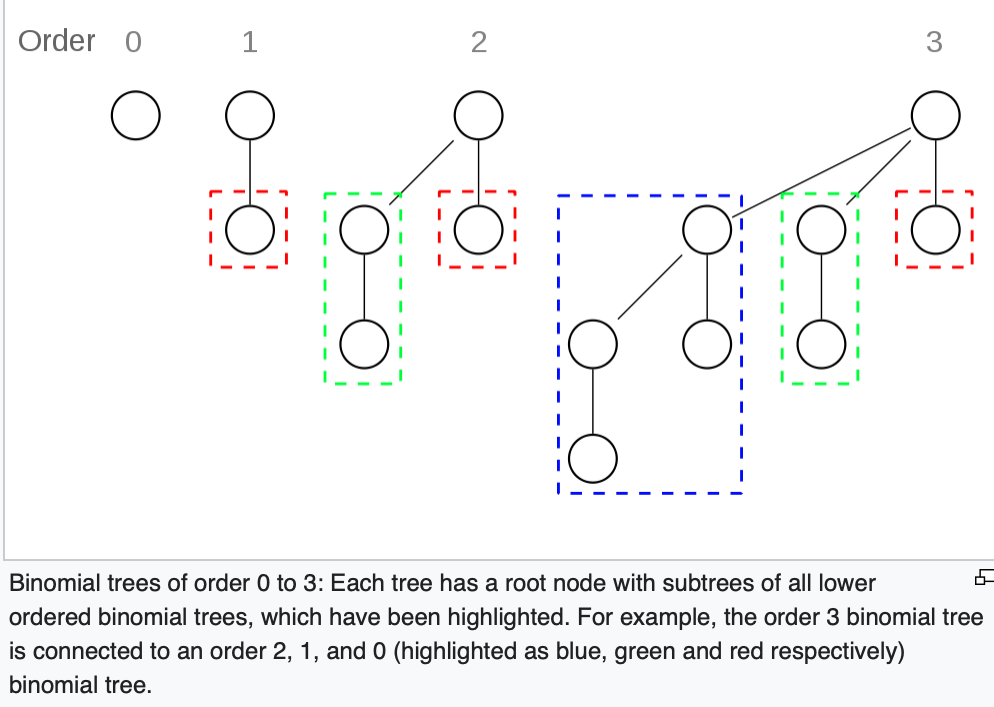
위의 그림에서 확인할 수 있듯, the order 3 binomial tree는 order 2, 1, 0 짜리와 연결된 구조를 갖는다.  또 a binomial tree of order k는 2^k의 nodes를 갖고 height: k 이다. 

 

=> A binomial tree of order k has (k,d) nodes at depth d : 여기서 이항계수가 등장하기 때문에 이름을 이항트리라고 부르는 것이다. 

 

 

 

 

Structure of a binomial heap

: A binomial heap is implemented as a set of binomial trees that satisfy the binomial heap properties

1) Each binomial tree in a heap obeys the minimum-heap property

 ( the key of a node is greater than or equal to the key of its parent.)

2) There can be at most one binomial tree for each order, including zero order.

 (각 트리의 오더는 서로 겹치지 않는다. -> 한 order당 트리는 at most 하나!!)

 

첫번째 규칙은 각각 Binomial trees의 루트가  해당 트리에서 가장 작은 key를 가지고 있으면 된다. It follows that the smallest key in the entire heap is one of the roots.

 

두번째 규칙은 a binomial heap with n nodes 가 최대 at most 1+log2(n) 개의 binomial trees로 구성되었음을 시사한다. The number and orders of these trees are uniquely determined by the number od nodes n.

 

 

예를 들면 13의 이진수는 1101 (8+4+1)

따라서 a binomial heap with 13 nodes는 order가 3,2, and 0 인 총 3개의 binomial trees 으로 구성된다.

 

 

 

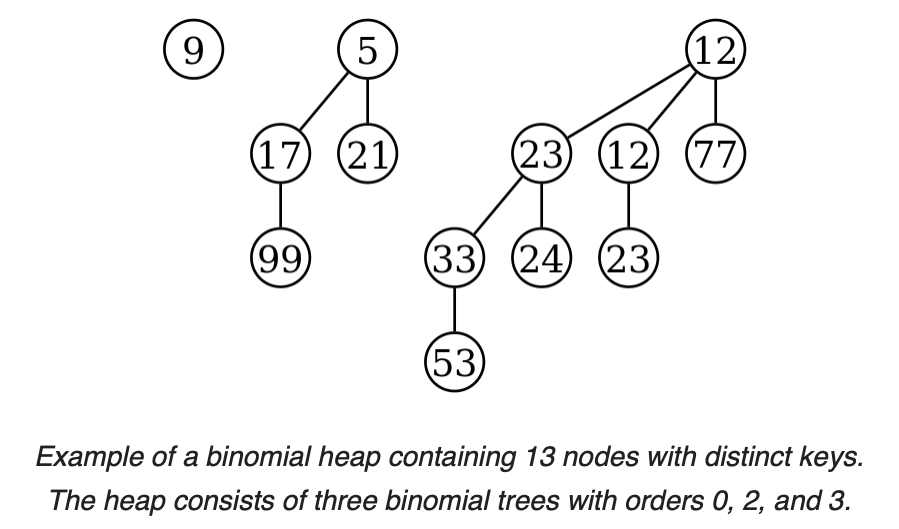
=> 한 숫자당 이진수 하나가 맵핑되는 것처럼, binomial tree에서도 node의 갯수가 하나 정해지면 이진수 계산법에 따라서 해당 orderd을 갖는 tree를 배정해주면 된다. 예를 들어서 만약 node의 갯수가 5인 binomial tree를 구성한다고 하면, 5 = 4+0+1. 즉, 이진수로 나타냈을 때 101 이다. 따라서 order가 2,0인 트리 두 개로 구성해주면 된다.

(order:2인 트리에서 노드 4개를 차지, order:0인 트리에서 노드를 1개 차지하므로 총 5개의 노드가 생성되는 것이다.)

 

 

 

 

 

Implementation

 

1.  Merge

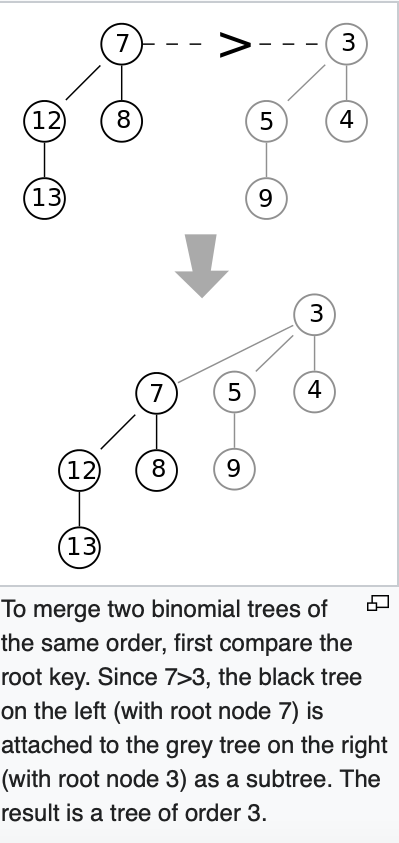
The operation of merging two heaps is used as a subroutine in most otehr operations. A basic subroutine within this procedure merges pairs of binomial tress of the same order. This may be done by comparing the keys at the roots of the two trees.(root means the smallest keys in both trees) The root node with the larger key is made into a child of the root node with the smallest key, including its order by one.

=> order가 같은 트리에 대해서 merge를 진행하는데 root의 크기를 비교하고 더 큰 루트를 가진 쪽이 서브트리가 되는 방식으로 진행된다.

function mergeTree(p, q)
    if p.root.key <= q.root.key
        return p.addSubTree(q)
    else
        return q.addSubTree(p)

 

 

 

 

2. Insert

Inserting a new element to a heap can be done by simply creating a new heap containing only this elelment and then merging it with the original heap. => 삽입 연산은 단지 넣고 싶은 elelment만 가지고 있는 트리를 새로 만들고, 기존의 트리와 merge 연산을 진행하면 삽입 결과를 얻을 수 있다. 

Because of the merge, a single insertion takes time O(log n). However, this can be sped up using a merge procedure that shortcuts the merge after it reaches a point where only one of the merged heaps has tress of larger order. 

 

 

 

3. Find minimum

To find the minimum elelments of the heap, find the minimum among the roots of the binomial trees. by using a pointer to the binomial tree that contains the minimum element, the time for this operation can be reduced to O(1). 

 

 

 

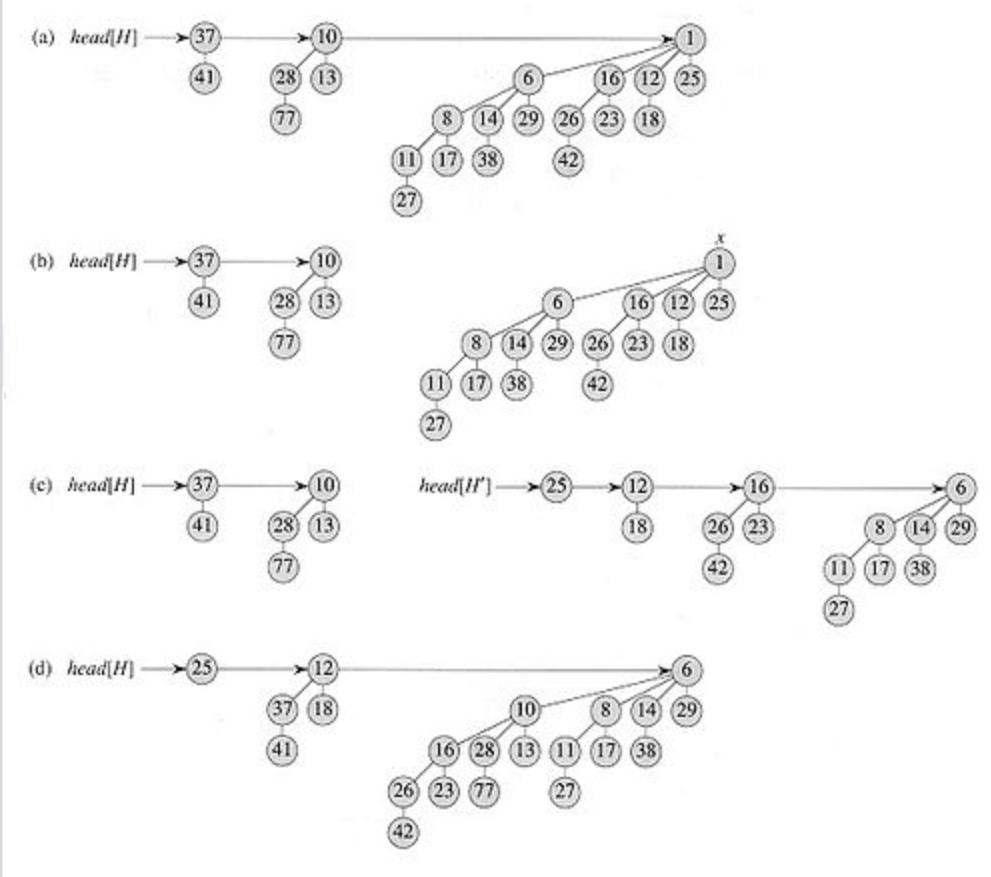
4. Delete minimum

To delete the minimum element from the heap, first find this element, remove it from the root of its binomial tree, and obtain a list of its child subtrees. Transform this list of subtrees into a separate binomial heap by reordering them from smallest to largest order. Then merge this heap with the original heap. Since each root has at most log2(n) children, creating this new heap takes time O(log n). Merging heaps takes time O(log n), so the entire delete minimum operation takes time O(log n).

 

해당 원소 찾기 -> 해당 원소를 그 binomial tree의 루트로 부터 제거하기 -> 제거한 루트의 child subtrees의 리스트 얻기 -> child subtree의 리스트를 가장 작은 order ~ 가장 큰 order 순으로 재배열해서 분리된 binomial heap으로 변환하기. -> 다음 original heap과 merge.